The Poor Pigs Problem
Introduction
This is an interesting problem I ran across on leetcode.com. I have included the description of it below.
There are 1000 buckets, one and only one of them contains poison, the rest are filled with water. They all look the same. If a pig drinks that poison it will die within 15 minutes. What is the minimum amount of pigs you need to figure out which bucket contains the poison within one hour.
Answer this question, and write an algorithm for the follow-up general case.
Follow-up:
If there are n buckets and a pig drinking poison will die within m minutes, how many pigs (x) you need to figure out the “poison” bucket within p minutes? There is exact one bucket with poison.
Additional Clarfications
I am going to work with the following details:
A pig has infinite speed when it comes to drinking from the buckets (ie: you can have one pig drink from all 1000 buckets in as short amount of time as you need and still receive a fatal dose).
If a pig is poisoned it dies sometime within 15 minutes instead of at exactly the 15-minute mark. This ensures that you cannot use the trivial solution where you find the poisoned bucket by getting only one pig to quickly drink all 1000 buckets and figure out the poisoned bucket by timing the pig’s death.
The Binary State Method
One Round of Testing
Disclaimer: I didn’t come up with this entirely by myself. Credit should also go to Ting Zheng.
First let’s start with a simplified case with a total number of n = 4 buckets and only one round of testing.
Buckets: A, B, C, D
Now take x = 2 pigs and divide the buckets as follow:
P1: A, B
P2: B, C
No pigs: D
No matter which bucket contains the poison you can always deduce it by looking at the combination of dead/alive states of P1 and P2 after 15 minutes. This works because the total number of combinations using the binary states of each pig is \(2^2 = 4 \ge n\) .
This can be extended for a larger number of buckets as well, for example, for n = 16 buckets we can do it with 4 pigs:
Buckets: A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P
P1: A, B, C, D, E, F, G, H
P2: E, F, G, H, I, J, K, L
P3: A, B, E, F, I, J, M, N
P4: B, C, F, G, J, K, N, O
No Pigs: P
Here is a graphical representation of the above division of buckets to each pig:
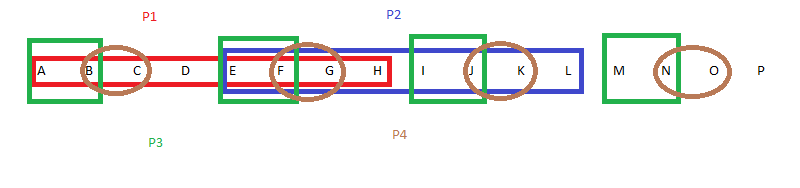
You can see that the buckets are divided into repeating sub-units of 4 similar to the 4-bucket case. Once again, total number of dead/alive combinations is \(2^4 = 16 \ge n\). In fact, for any n buckets you can find the poisoned one with a minimum of \(x = \lceil log_2(n) \rceil\) pigs (ie: the smallest x to satisfy \(2^x \ge n\)).
Four Rounds of Testing
Now we will consider the original question and allow four rounds per the original requirement. Let’s start with just a generalized number of buckets, n. Since we have 4 tries, we can start by cutting down the number of buckets that we have to test in detail as much as possible. We can do this by dividing the buckets into groups and test each group with just one pig to locate the group that contains the poison.
If we have x pigs in total, we can divide n buckets into (x + 1) groups (if no pigs die then it must be the group that isn’t tested). Since the question asks for a minimum x pigs that guarantees finding the poison, we need to be conservative here and consider only the worst case scenario where we lose as many pigs as possible. So in this first division we lose one pig and have (x - 1) pigs left.
We then repeat the process twice. Since we have lost a pig already, we can only divide into x groups now (and lose another pig in the process). Finally on the third division we have (x - 1) groups and lose one last pig. We now have (x - 3) pigs left and a group with approximately \(\frac{n}{(x + 1)(x)(x - 1)}\) buckets. These are the buckets that we must test in detail on the last round using the binary state combinations of the (x - 3) pigs we have left in order to locate the poisoned bucket (at most \(2^{x - 3}\) buckets).
Working backward, we can see that the minimum amount of pigs we need is the smallest x that satisfies the following:
\[\begin{equation} 2^{x-3}(x+1)(x)(x-1) \ge n \tag{1} \end{equation}\]where x = number of pigs and n = number of buckets.
Note that in order for eq (1) to make sense we must start with at least 4 pigs (otherwise you will run out of pigs in the worst case scenario). This means this particular method is only justified for a total number of buckets exceeding 120. For buckets less than 120 you may want to reduce the number of rounds dedicated to dividing buckets into groups and avoid losing pigs unnecessarily.
Back to the Original
With n = 1000, the minimum x that satisfies equation (1) is x = 6. In fact, with 6 pigs you can test up to a whopping 1680 buckets in an hour!
Follow Up
If pigs die within m minutes and we are given p minutes, then the number of test rounds is \(\lfloor\frac{p}{m}\rfloor\). Out of these, \(\lfloor\frac{p}{m}\rfloor - 1\) rounds are used to divide buckets into groups and zoom in on the general location of the poison. Equation (1) can then be generalized to
\[\begin{equation} 2^{x- \lfloor \frac{p}{m} \rfloor + 1}\prod_{i = 1}^{\lfloor \frac{p}{m} \rfloor - 1} (x + 2 - i) \ge n \tag{2} \end{equation}\]Digression
There is an interesting suggestion proposed by StephanPochmann. The suggestion essentially advocates arranging the buckets into 5x5 square matrices and use two pigs each to find the (x, y) coordinates of the poisoned bucket within four rounds of testing. If there are more than 25 buckets in total you can divide the buckets into units of 5x5 matrices and assign two pigs for each. It further postulates an extension of using 5 x 5 x 5 cubes and 3 pigs per cube. However, there are some problems:
While the method using square matrices is possible, the suggestion of further optimization using cubes is not. Suppose there is exactly one 5 x 5 x 5 cube of buckets and 3 pigs total for the 3 axis. Each pig can drink a max of 5 buckets on their respective axis. With 3 pigs you get 15 buckets tested per round. After 4 rounds you have only tested 15 x 4 = 60 buckets and that is assuming no buckets are tested multiple times. That leaves at least 65 buckets untested in each cube! If you want guaranteed results you can only leave at most 1 bucket untested out of all of the cubes.
If the total number of buckets requires more than one matrix units you cannot systematically leave one bucket untested in each matrix because again, only one untested buckets out of all of the matrices combined is allowed for guaranteed result. Therefore in the cases where you have more than one matrix unit each matrix can only be a 5 x 5 minus one of its corners (24 buckets in total) with the exception of a single full 5 x 5 matrix at the beginning.
Assuming p = 60 and m = 15 as per the original specification, since the number of buckets tested using the binary state method grows exponentially by the number of pigs, it quickly overtakes the matrix method in terms of efficiency as the number of buckets increases. Specifically, The matrix method can test 16 buckets using two pigs. Any n > 25 requires you to divide them into matrix groups. This means x is roughly \(2*\frac{n}{24}\) -> \(O(n)\). In comparison, the binary method is actually better than \(O(log(n))\) (see (1)).
