A Simplified Simulation
Let’s use a simulated data set to help us understand what may happen.
# Load all required libraries.
library("caret")
library("rpart")
library("rpart.plot")
set.seed(123)
toss <- rbinom(1000, 1, 0.5)
inst <- rnorm(1000) + toss
volt <- rnorm(1000)
water <- rnorm(1000)
toss_fac <- factor(toss, labels = c("tail", "head"))
data <- data.frame(inst = inst, volt = volt, water = water, response = toss_fac)The response is 1000 tosses drawn from a binomial distribution and factored into either tail or head. The predictors are
- The
instrument measurement modeled simply as the response + a normally distributed signal noise. - The deviation in
voltage in the electrical circuits of the house. Modeled as a standard normal distribution. - The deviation in
waterpressure of the house. Modeled as a standard normal distribution.
The data is then split into training and vadliation sets.
inTrain <- createDataPartition(toss_fac, p = 0.6, list = FALSE)
data.train <- data[inTrain, ]
data.validation <- data[-inTrain, ]I am now going to train three decision tree models using the training sets, each demonstrating a different aspect.
Model 1: Overtly Sensitive to Instrument Noise.
This model will use a huge amount of splitting and very small leafs to fit the training data. The goal of this model is to achieve very high accuracy on the training set using the instrument measurement without any concerns for potentially overfitting.
First we will set up the hyper-parameters for the tree model.
treeCon.over <- rpart.control(minsplit = 2, minbucket = 1, cp = 0, xval = 10)The exact meaning of the parameters are not super important but here it is:
minsplit: controls how many training data points a node has to have before the algorithm can attempt to grow branches from it.
minbucket: how many training data points a leaf must at least have in the final tree.
cp: controls how good a branch must be before it can be kept. Each branch must increase model quality (ie: R^2) by at least cp or it will be cut-off.
xval: number of cross-validation folds to be used for pruning (this will make sense later).
So with this in mind, our tree is pretty much set up to be as complex as possible. Here’s the code to build the model:
set.seed(1)
tree1 <- rpart(response ~ inst, data = data.train, control = treeCon.over)Notice that I have thrown away the other stuff Mike collected such as voltage and water pressure. The model is built using the noisy instrument signal as its sole predictor. Let us plot the tree structure.
rpart.plot(tree1)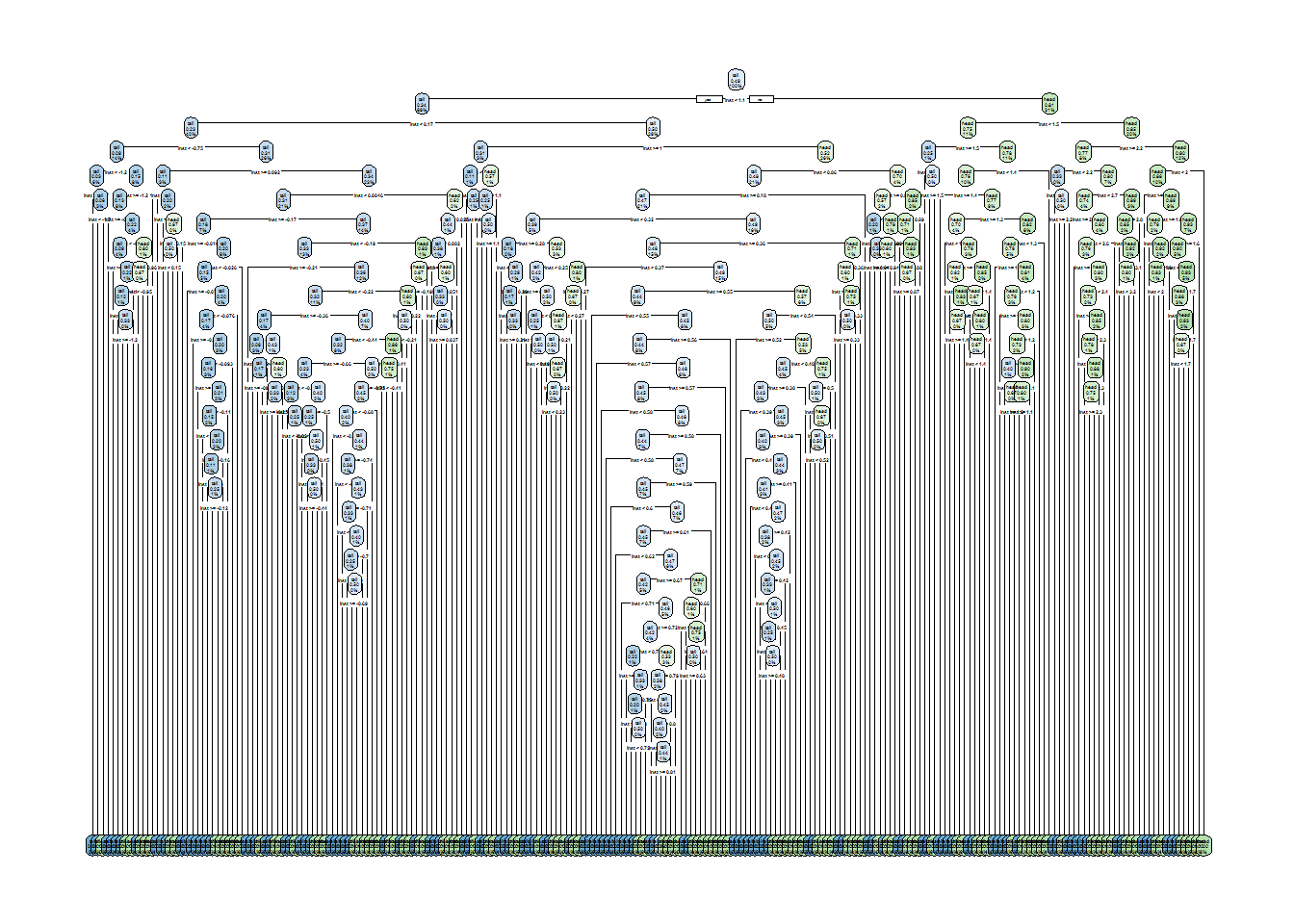
Whoa! That is indeed an extremely complex tree. However, what will the effect be on training set accuracy? Let’s find out:
pred.train1 <- predict(tree1, data.train, type = "class")
conMat1 <- confusionMatrix(pred.train1, data.train$response)
conMat1## Confusion Matrix and Statistics
##
## Reference
## Prediction tail head
## tail 305 3
## head 0 293
##
## Accuracy : 0.995
## 95% CI : (0.9855, 0.999)
## No Information Rate : 0.5075
## P-Value [Acc > NIR] : <2e-16
##
## Kappa : 0.99
## Mcnemar's Test P-Value : 0.2482
##
## Sensitivity : 1.0000
## Specificity : 0.9899
## Pos Pred Value : 0.9903
## Neg Pred Value : 1.0000
## Prevalence : 0.5075
## Detection Rate : 0.5075
## Detection Prevalence : 0.5125
## Balanced Accuracy : 0.9949
##
## 'Positive' Class : tail
## An accuracy of 0.9950083. That is extremely high. Should we choose this one as our final model? Let’s build a couple other models first.
Model 2: Selected Useless Features
Let’s change some hyper-parameters:
treeCon <- rpart.control(minsplit = 10, minbucket = 3, cp = 0.01, xval = 10)So we have made each branching node and leaf larger, with also a higher quality improvement requirement during pruning. Let’s build the model now.
set.seed(1)
tree2 <- rpart(response ~ inst + volt + water, data = data.train, control = treeCon)Notice that although our hyper-parameters demand an overall decrease in structural complexity of the tree, we are now also using the other features Mike collected such as voltage and water pressure deviations to construct the model. Here’s the final strucutre:
rpart.plot(tree2)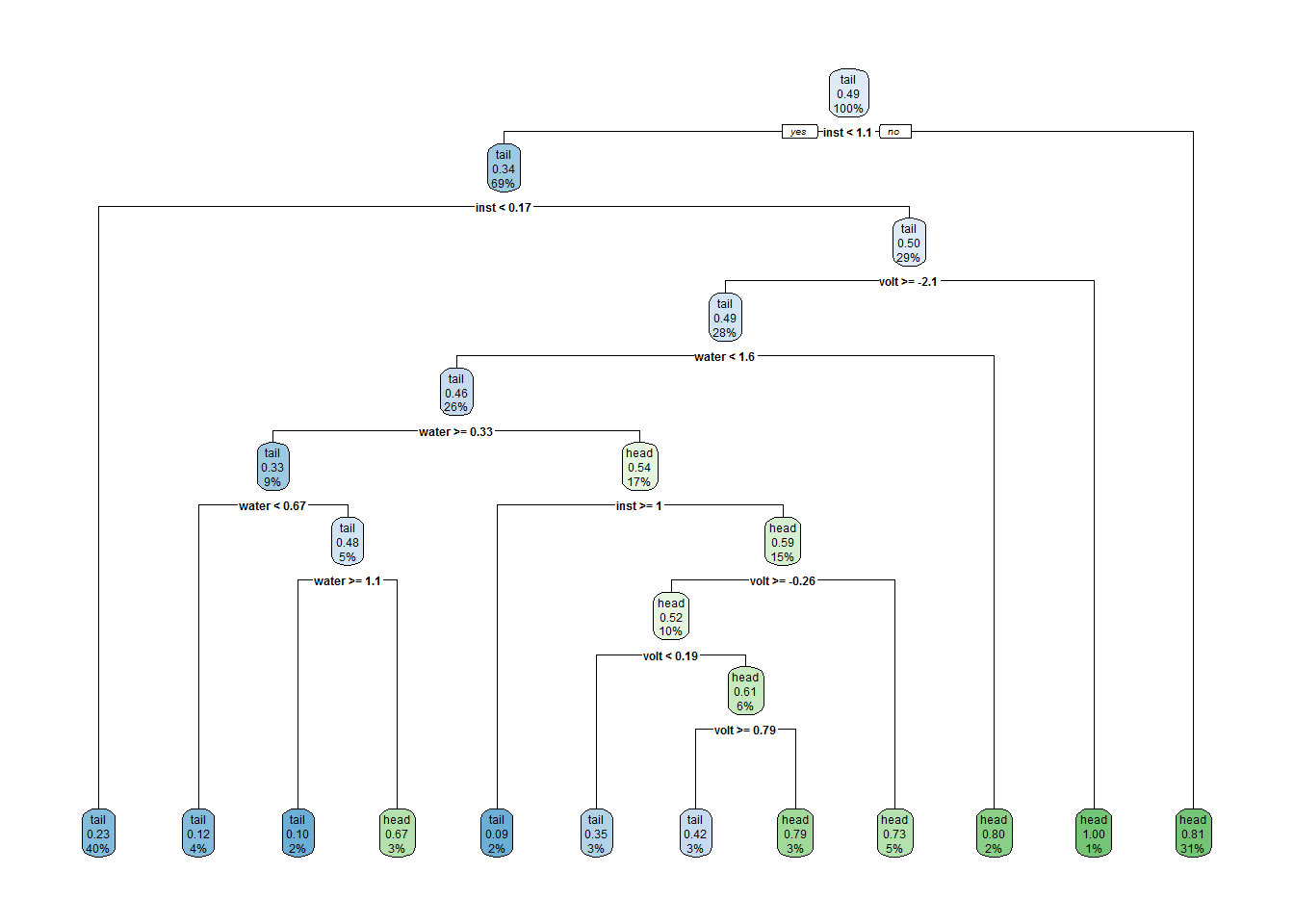
As expected, this is a much simpler tree in terms of sturctural complexity (albeit still pretty complex). However it does make use of all three features, some of them we suspect to be useless. What about its training set accuracy?
pred.train2 <- predict(tree2, data.train, type = "class")
conMat2 <- confusionMatrix(pred.train2, data.train$response)
conMat2## Confusion Matrix and Statistics
##
## Reference
## Prediction tail head
## tail 248 76
## head 57 220
##
## Accuracy : 0.7787
## 95% CI : (0.7434, 0.8113)
## No Information Rate : 0.5075
## P-Value [Acc > NIR] : <2e-16
##
## Kappa : 0.5569
## Mcnemar's Test P-Value : 0.1186
##
## Sensitivity : 0.8131
## Specificity : 0.7432
## Pos Pred Value : 0.7654
## Neg Pred Value : 0.7942
## Prevalence : 0.5075
## Detection Rate : 0.4126
## Detection Prevalence : 0.5391
## Balanced Accuracy : 0.7782
##
## 'Positive' Class : tail
## With an accuracy of 0.7787022 it seems to be markedly worse than model 1…or is it? At the very least it still has quite a bit of predictive power since it’s accuracy is significantly higher than the No Information Rate. Let’s build one final model.
Simple structure with only the relevant feature.
No changes will be made to the hyper-parameters here. Instead, we will train the model with just one difference:
set.seed(1)
tree3 <- rpart(response ~ inst, data = data.train, control = treeCon)This tree is built with the same complexity parameters as our last tree, but only using the instrument measurements as its feature. Let’s check out its structure:
rpart.plot(tree3)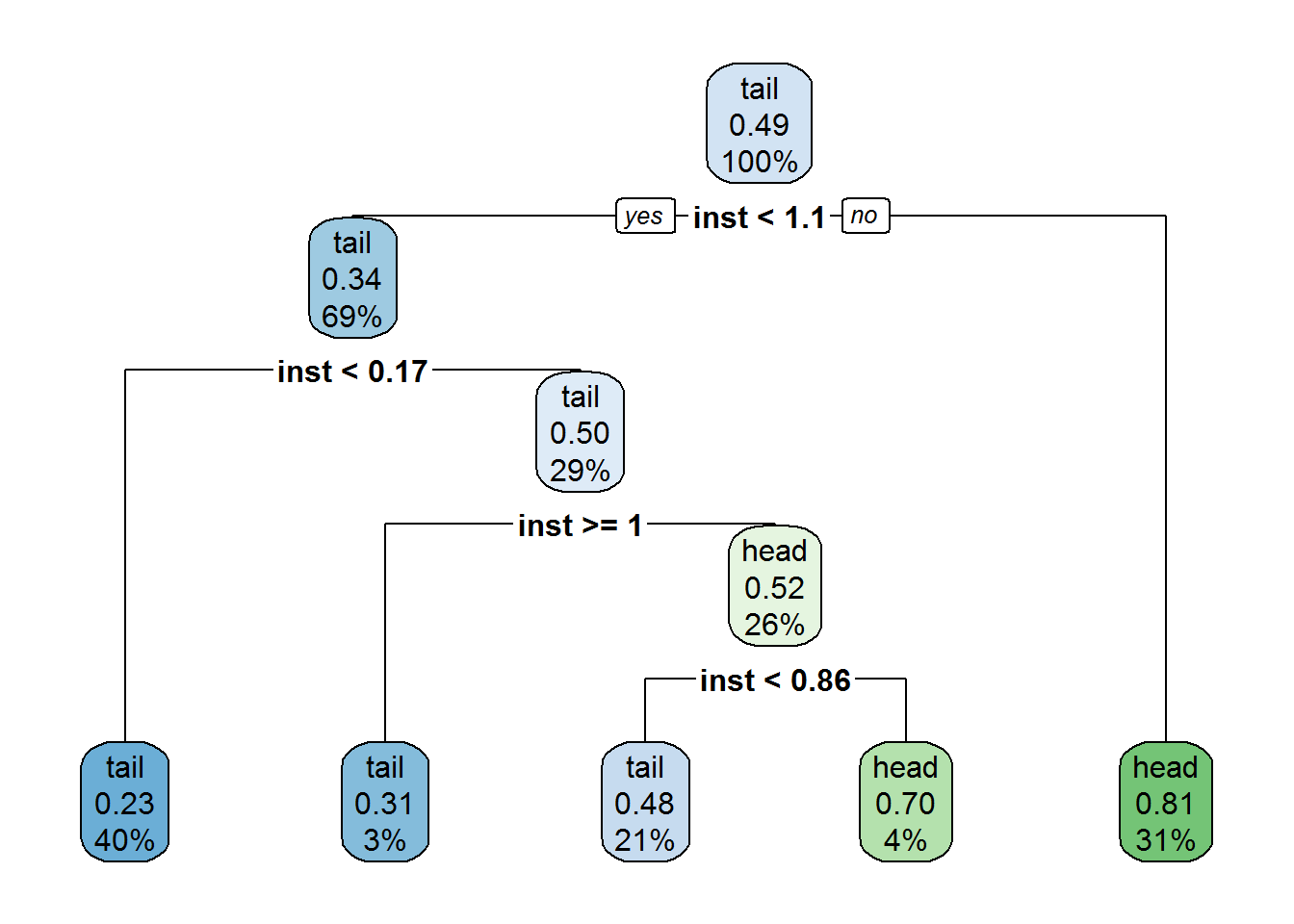
Clearly this is the simplest tree by far in terms of both structure and feature usage. How about its accuracy on the training set?
pred.train3 <- predict(tree3, data.train, type = "class")
conMat3 <- confusionMatrix(pred.train3, data.train$response)
conMat3## Confusion Matrix and Statistics
##
## Reference
## Prediction tail head
## tail 262 123
## head 43 173
##
## Accuracy : 0.7238
## 95% CI : (0.6862, 0.7592)
## No Information Rate : 0.5075
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.4453
## Mcnemar's Test P-Value : 8.701e-10
##
## Sensitivity : 0.8590
## Specificity : 0.5845
## Pos Pred Value : 0.6805
## Neg Pred Value : 0.8009
## Prevalence : 0.5075
## Detection Rate : 0.4359
## Detection Prevalence : 0.6406
## Balanced Accuracy : 0.7217
##
## 'Positive' Class : tail
## Uh oh. With an accuracy of 0.7237937 this is by far the worst model we have built! I guess it’s clear we should use the big tree from model 1 as our final model, right? Oh wait, we split the data into training and validation set! Since the models are all built on the training set they have no ideas what the validation set looks like. If we feed the models the validation set we can make actual predictions with them and get a sense on its predictive accuracy. How exciting! Let’s do it.
Performance Evaluation (Validation)
Here’s the code to make predictions on the validation set and compute the prediction statistics:
pred.validation.1 <- predict(tree1, data.validation, type = "class")
pred.validation.2 <- predict(tree2, data.validation, type = "class")
pred.validation.3 <- predict(tree3, data.validation, type = "class")
confMat.valid.1 <- confusionMatrix(pred.validation.1, data.validation$response)
confMat.valid.2 <- confusionMatrix(pred.validation.2, data.validation$response)
confMat.valid.3 <- confusionMatrix(pred.validation.3, data.validation$response)I am just going to list the accuracies below in a table:
df <- data.frame(Model = c("Model 1", "Model 2", "Model 3"), Accuracy = c(confMat.valid.1$overall[1],
confMat.valid.2$overall[1], confMat.valid.3$overall[1]))
kable(df)| Model | Accuracy |
|---|---|
| Model 1 | 0.6065163 |
| Model 2 | 0.6691729 |
| Model 3 | 0.6791980 |
Well well. The table has turned! The big tree in model1, although has an amazing training set accuracy, is now the definitive last place when it comes to making predictions on the validation set. The tree with the worst training set performance, the tree with low complexity parameters and only using the instrument measurement as its feature, is now the best performer. Why is that?
By now you probably have a good idea to the answer already. The first two trees overfit the data (especially the first one). The first tree contains too many nodes and leafs. The result is it is able to almost fit each data point in the training set into single leafs by themselves and simply look them up on the training set. No wonder it has such amazing training set accuracy. However, when it comes to making actual predictions on the validation set all the noise throws it off and causes it to overreact on noisy signals that don’t have any real effect on the response. The result is terrible predictive accuracy.
Although the second tree tries to avoid very complex structure, it uses features that are clearly useless in predicting the response (water pressure and voltage deviations…really, Mike?). The good thing is the pruning process is able to catch some of these and cut them off the trees so it doesn’t make too much of a negative impact on its prediction accuracy.
Nevertheless, you can see that model 3, with the simplest structure and using only the relevant feature, turns out to be the best one in the end. The simple structure is achieved by tuning hyper-parameters and the art of using only relevant features is called feature selection. In this case, these steps are largely done by experience and logic. I know before hand that the data is noisy and two of the features are useless, so all I need to do is just selecting sensible values relative to my other choices and get rid of useless features. This is actually an excellent way to build models in reality as it is not information obtained directly using the data so there is no risk of overfitting.
The truth is, whenever you are using the data to gain information about what your model should be, what features you shoud select etc, you can potentially overfit. The biggest problem with overfitting is it contaminates your performance assessment and can cause you to make the wrong choice (see the inflated training set accuracies of all three models). For example, now I know the prediction accuracies of the three models on the validation set, if I go back, tweak some parameters/select some features and retrain the model on the training set to maximize my prediction accuracy on the validation set, the validtion set accuracy is likely going to be biased due to overfitting. Why? Because the accuracy assessment on the validation set is information gleaned from the validation set. By going back to make model tweaks based on it, information in the validation set is now spilling over to the model training process and the validation set accuracy will likely become biased just like the training set accuracies. There are ways to avoid or at least minimize the bias. We shall see that in another post.